Heatmap Regression without Soft-argmax for Facial Landmark Detection
Purdue University, Department of Computer Science
ICCV 2025
TLDR
- $\tt Soft\text{-}argmax$ approximation is unnecessary and suboptimal for heatmap regression.
- Without $\tt Soft\text{-}argmax$, our method is competitive while achieving a 2.2$\times$ faster training convergence.
Abstract
Facial landmark detection is an important task in computer vision with numerous applications,
such as head pose estimation, expression analysis, face swapping, etc.
Heatmap regression-based methods have been widely used to achieve state-of-the-art results in this task.
These methods involve computing the argmax over the heatmaps to predict a landmark. Since $\tt argmax$ is not differentiable,
these methods use a differentiable approximation, $\tt Soft\text{-}argmax$, to enable end-to-end training on deep-nets.
In this work, we revisit this long-standing choice of using $\tt Soft\text{-}argmax$ and demonstrate that it is not the only way to achieve strong performance.
Instead, we propose an alternative training objective based on the classic structured prediction framework.
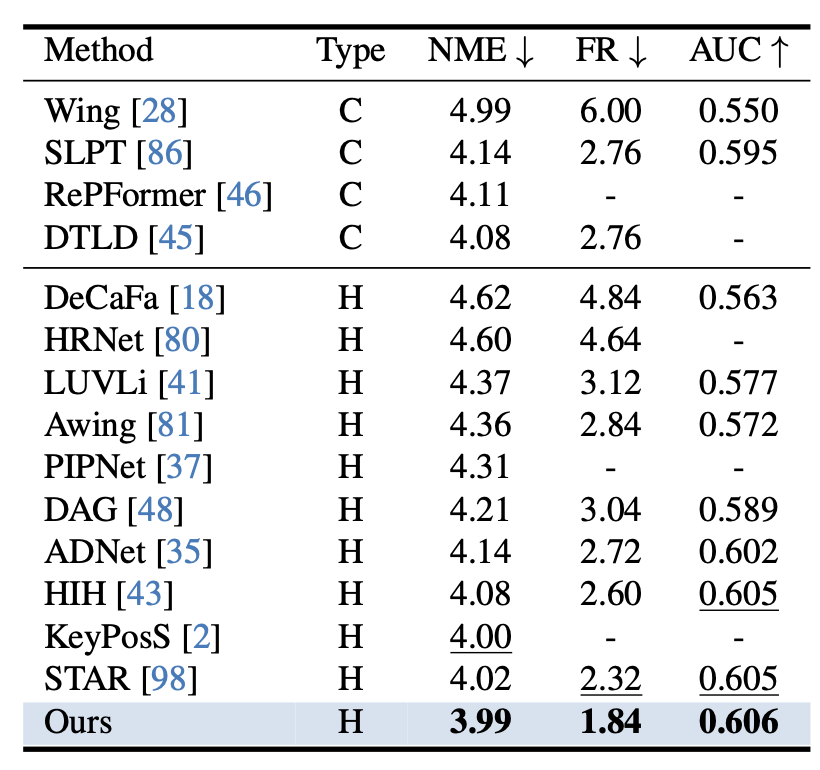
Empirically, our method achieves state-of-the-art performance on three facial landmark benchmarks (WFLW, COFW, and 300W),
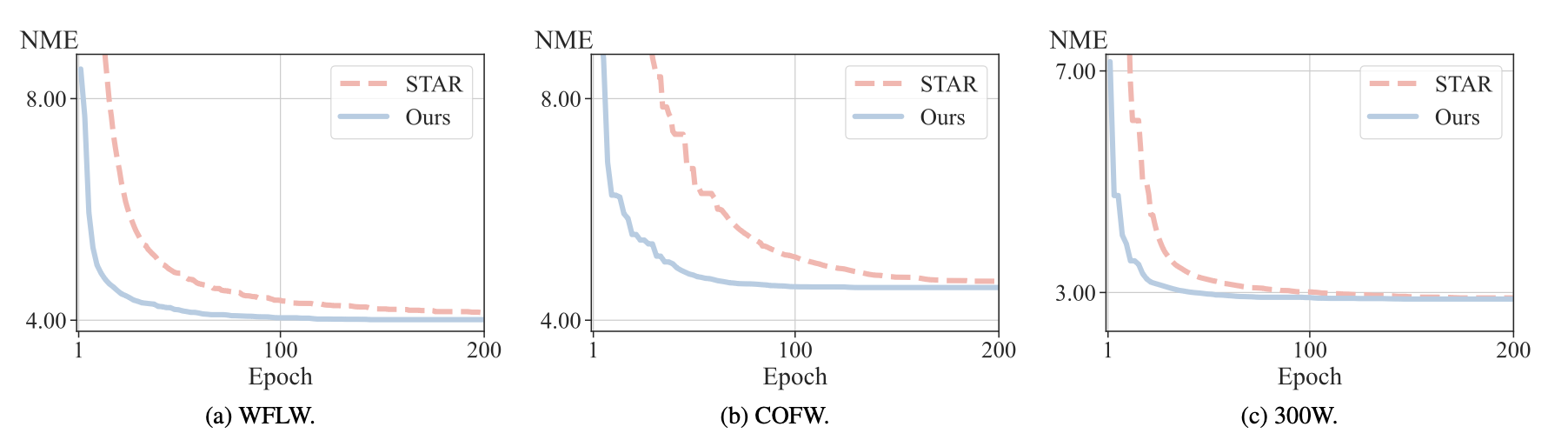
converging $2.2\times$ faster during training while maintaining better and competitive accuracy.
Approach
Let $\mathbf{X} \in \mathbb{R}^{3 \times H \times W}$ to be an input facial image labeled with $N$ landmarks $\mathbf{y} = [\mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_N]$,
where each $\mathbf{y}_n$ represents the pixel location $(u,v) \in \{0, \dots, H-1\}\times \{0, \dots, W-1\}$ of the landmark, i.e., $\mathbf{y} \in \mathbb{R}^{N \times 2}$.
The task of landmark detection is to learn a model, parameterized by $\theta$, that predicts landmark $\hat{\mathbf{y}}$ given the input face image $\mathbf{X}$.
In heatmap regression methods, given an input, the model outputs $N$ heatmap $\hat{\mathbf{H}} = [\hat{\mathbf{H}}_1, \dots, \hat{\mathbf{H}}_N] \in \mathbb{R}^{N\times H \times W}$
where each heatmap $\hat{\mathbf{H}}_n$ represents a score of each pixel being a landmark.
They are often trained by minimizing the distance between a soft approximation of the landmark coodinates $\tilde{\mathbf{y}}_n$ and the ground truth $\mathbf{y}_n$,
\begin{align}
\sum_n \|\tilde{\mathbf{y}}_n - \mathbf{y}_n\|_2^2.
\end{align}
where the $\tilde y_n$ is approximated from the heatmap $\hat{\mathbf{H}}_n$ using $\tt Soft\text{-}argmax$,
\begin{align}
\tilde{\mathbf{y}}_n = {\tt Soft\text{-}argmax}(\hat{\mathbf{H}}_n) \triangleq \sum_{\mathbf{y}'} \mathbf{y}' \cdot \texttt{Softmax}(\hat{\mathbf{H}}_n)[\mathbf{y}'],
\end{align}
Inspired by the well-studied structure prediction research, we propose the following loss to replace the $\tt Soft\text{-}argmax$ approximation in heatmap regression methods,
\begin{align}
\epsilon \ln \left(\sum_{\hat{\mathbf{y}}_n} \exp \frac{\Delta(\mathbf{y}_n, \hat{\mathbf{y}}_n) + F_n(\hat{\mathbf{y}}_n, \mathbf{X}, \theta)}{\epsilon}\right) - F_n(\mathbf{y}_n, \mathbf{X}, \theta).
\end{align}
Here we define $F_n(\mathbf{y}_n,\mathbf{X};\theta)$ as the scoring function of each possible coordinates for each landmark and $\Delta$ is an margin function of choice, e.g. $\ell_1$, $\ell_2$.
Demonstration
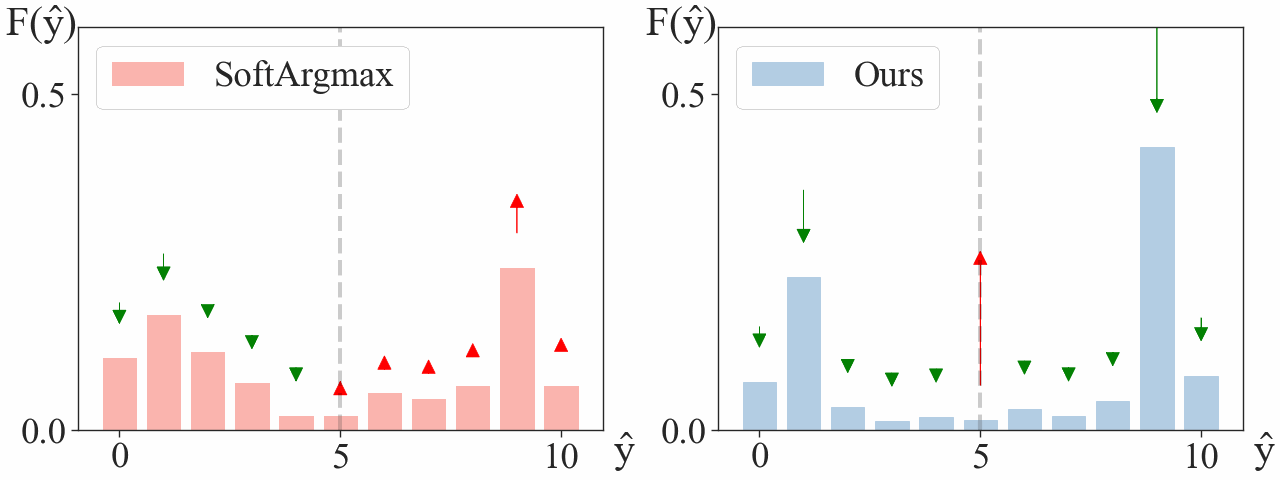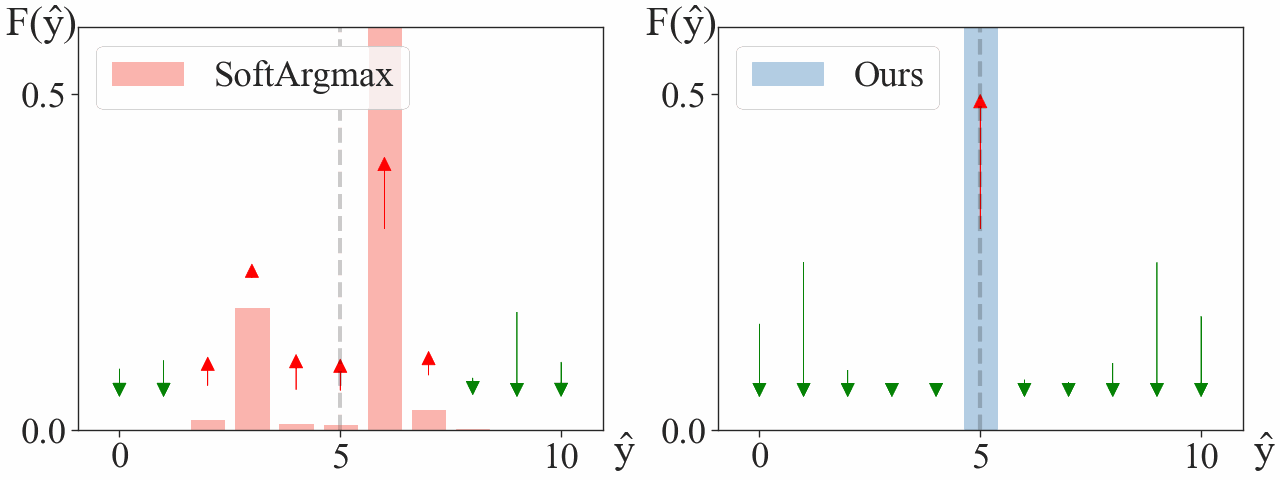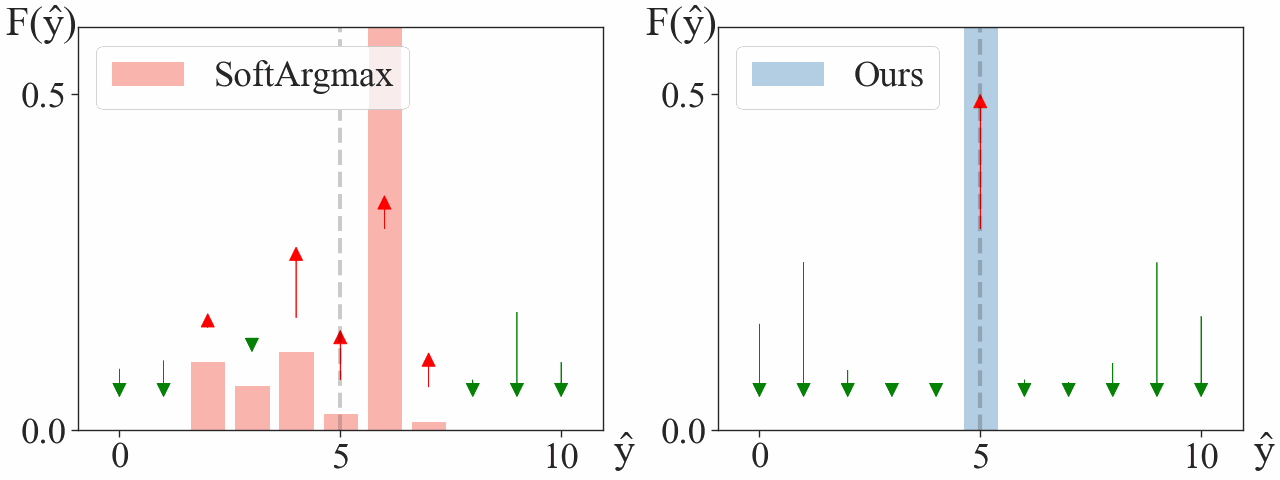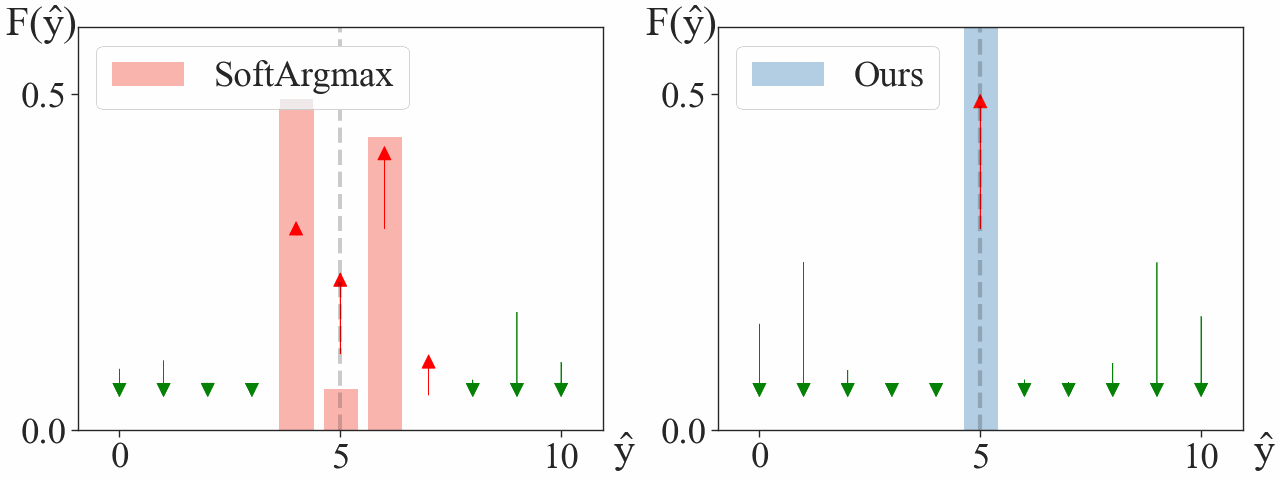
We consider a simplified model with a single landmark on a 1D heatmap. We choose the dataset to have a single training sample at ground truth $\mathbf{y} = 5$. We visualize how gradient descent updates the heatmap,
After a few steps, our argmax is already located at $\mathbf{y}=5$, with a significant gap between its maximum and second maximum. Meanwhile, Soft-argmax is still struggling to find the correct maximum.
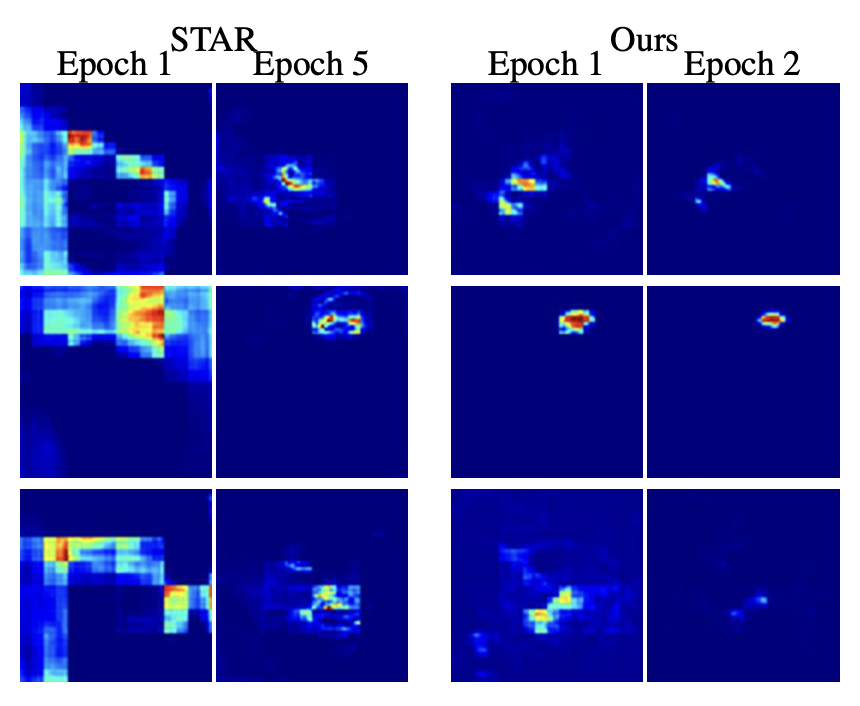
We observe signigicantly faster convergence when using our approach. In abstract, Soft-argmax gradually “moves” the peaks towards the target $\mathbf{y} = 5$, while ours directly increases the peak at the target while decreasing the others.
Citation
@inproceedings{yang2025regression,
title={Heatmap Regression without Soft-Argmax for Facial Landmark Detection},
author={Yang, Chiao-An and Yeh, Raymond A},
booktitle={Proc. ICCV},
year={2025}
}