Toward Long-Tailed Online Anomaly Detection through Class-Agnostic Concepts
1Purdue University, Department of Computer Science
2Mitsubishi Electric Research Laboratories
ICCV 2025
TLDR
- We propose the task and benchmark for long-tailed online AD (LTOAD);
- We propose a class-agnostic AD framework that does not require class information whatsoever.
Abstract
Anomaly detection (AD) identifies the defect regions of a given image. Recent works have studied AD, focusing on
learning AD without abnormal images, with long-tailed distributed training data, and using a unified model for all
classes. In addition, online AD learning has also been explored.
In this work, we expand in both directions to a realistic setting by considering the novel task of long-tailed
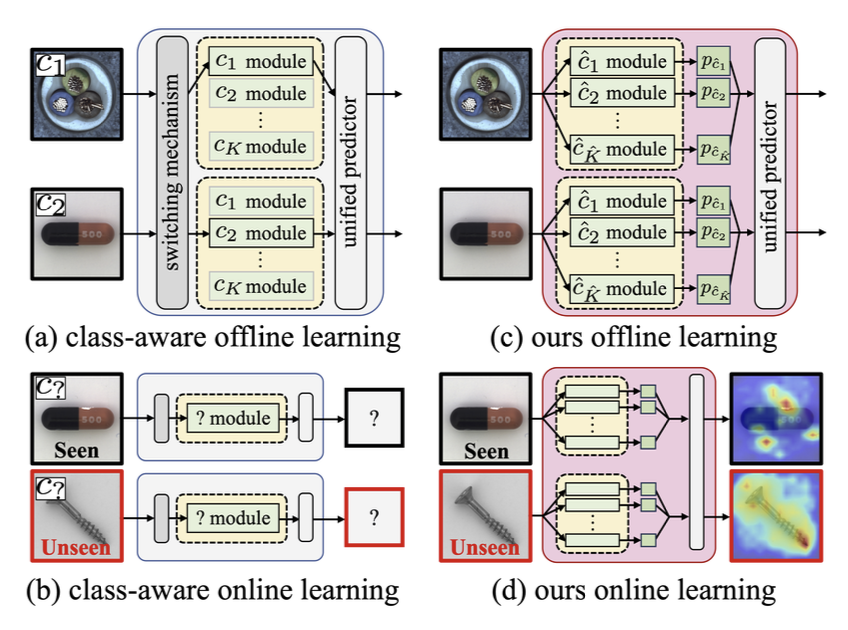
online AD (LTOAD). We first identified that the offline state-of-the-art LTAD methods cannot be directly applied to the
online setting. Specifically, LTAD is class-aware, requiring class labels that are not available in the online setting. To
address this challenge, we propose a class-agnostic framework for LTAD and then adapt it to our online learning set-
ting. Our method outperforms the SOTA baselines in most offline LTAD settings, including both the industrial manu-
facturing and the medical domain. In particular, we observe +4.63% image-AUROC on MVTec even compared to
methods that have access to class labels and the number of classes. In the most challenging long-tailed online setting,
we achieve +0.53% image-AUROC compared to baselines.
Making LTAD class-agnostic
Given an image $\mathbf{X}$, an AD model $F_\theta$ , parametrized by $\theta$,
aims to predict an abnormal map $\widehat{\mathbf{Y}}$ or an abnormal label $\hat{y}$ indicating whether the image is abnormal or not.
$$
\widehat{\mathbf{Y}}_i = F_\theta(\mathbf{X}_i)
$$
Class-aware AD methods assume that the class $c$ of the input image is also provided to the model.
$$
\widehat{\mathbf{Y}}_i = F_\theta(\mathbf{X}_i, c_i)
$$
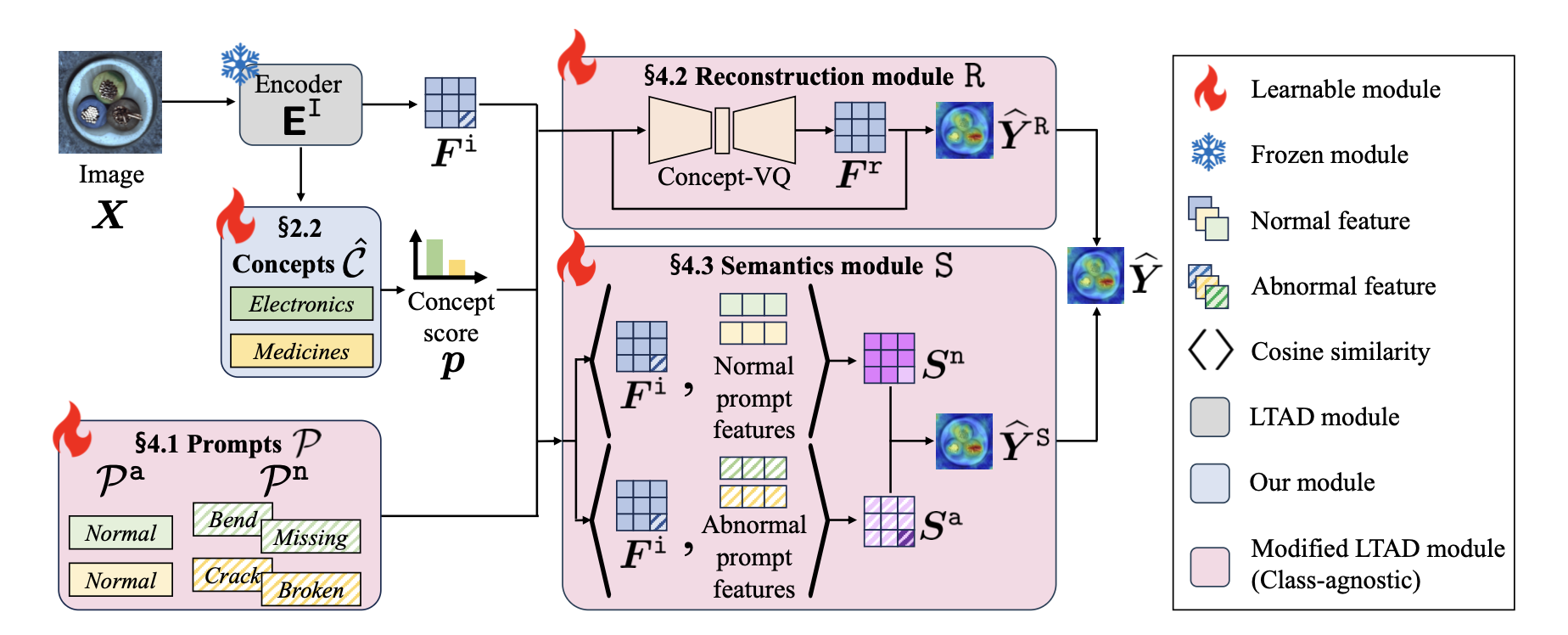
To remove the requirement of having $c$, we introduce a concept set $\widehat{\mathcal{C}}$
where we assume that the class information $c$ can be represented as a composition of multiple concepts in $\widehat{\mathcal{C}}$.
For example, the class $\it{transistor}$ is related to and derived from concepts $\it{semiconductors}$ and $\it{circuits}$.
In other words, for each image of class $c$, instead of applying a hard one-hot label,
we employ a soft weighting mechanism and assign a soft label $p \in \mathbb{R}^{\hat K}$ where $\hat K = |\widehat{\mathcal{C}}|$.
For this approach to be effective, the concept set $\widehat{\mathcal{C}}$ should be representative enough to cover the image classes ${\mathcal{C}}$ of interest.
Instead of manually selecting the set $\widehat{\mathcal{C}}$,
we leverage the zero-shot capability of foundation models
where $\widehat{\mathcal{C}}$ is
learned with only the visual information of the training set and without seeing any class labels.
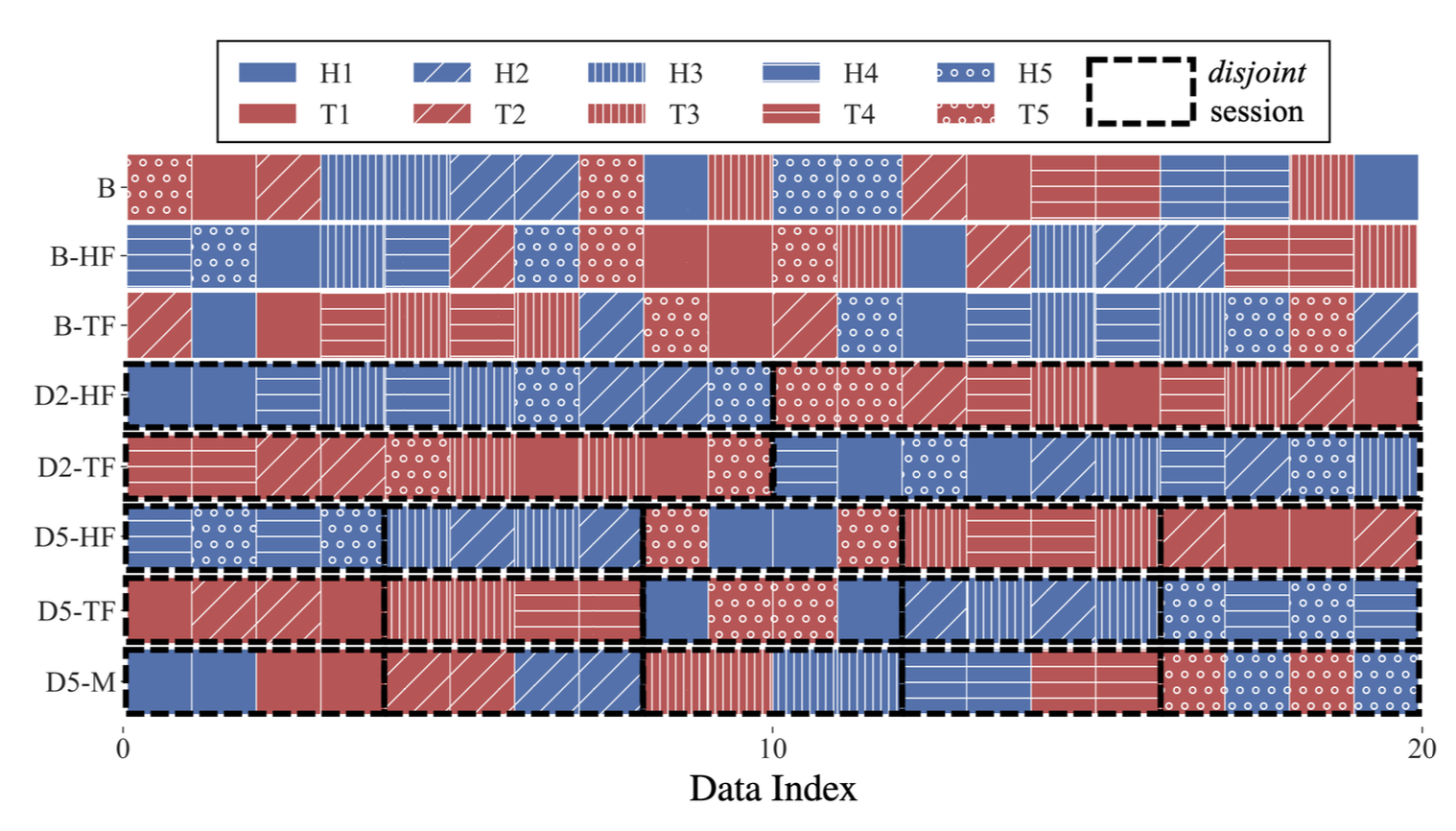
LTOAD benchmark
Given a model $F_{\theta_0}$ where $\theta_0$ is the parameters trained offline on an LTAD dataset,
the goal of LTOAD is to update the parameters $\theta_t$ in an online manner to improve the performance on a data stream
$\widetilde{\mathbf{X}}_{\leq t} = \left[ \widetilde{\mathbf{X}}_1,···, \widetilde{\mathbf{X}}_t \right] $ where each image $\widetilde{\mathbf{X}}$ comes sequentially.
Formally, we focus on improving the accuracy of $F_{\theta_t}(\widetilde{\mathbf{X}}_{\leq t}) = \hat{\mathbf{Y}_t}$ where $\hat{\mathbf{Y}}_t$ is the prediction at $t$.
Note that $\widetilde{\mathbf{X}}_{\leq t}$ is an ordered list, i.e., LTOAD is evaluated sequentially.
We consider the any-$\Delta$ inference setting where the model is updated on small batches of data samples of size $\Delta$.
As the data comes in a stream, a model's online learning performance is highly related to the ordering data.
To study the effect, we sequentially split the data stream into sessions which corresponds to a sublist of the dataset.
Experiments
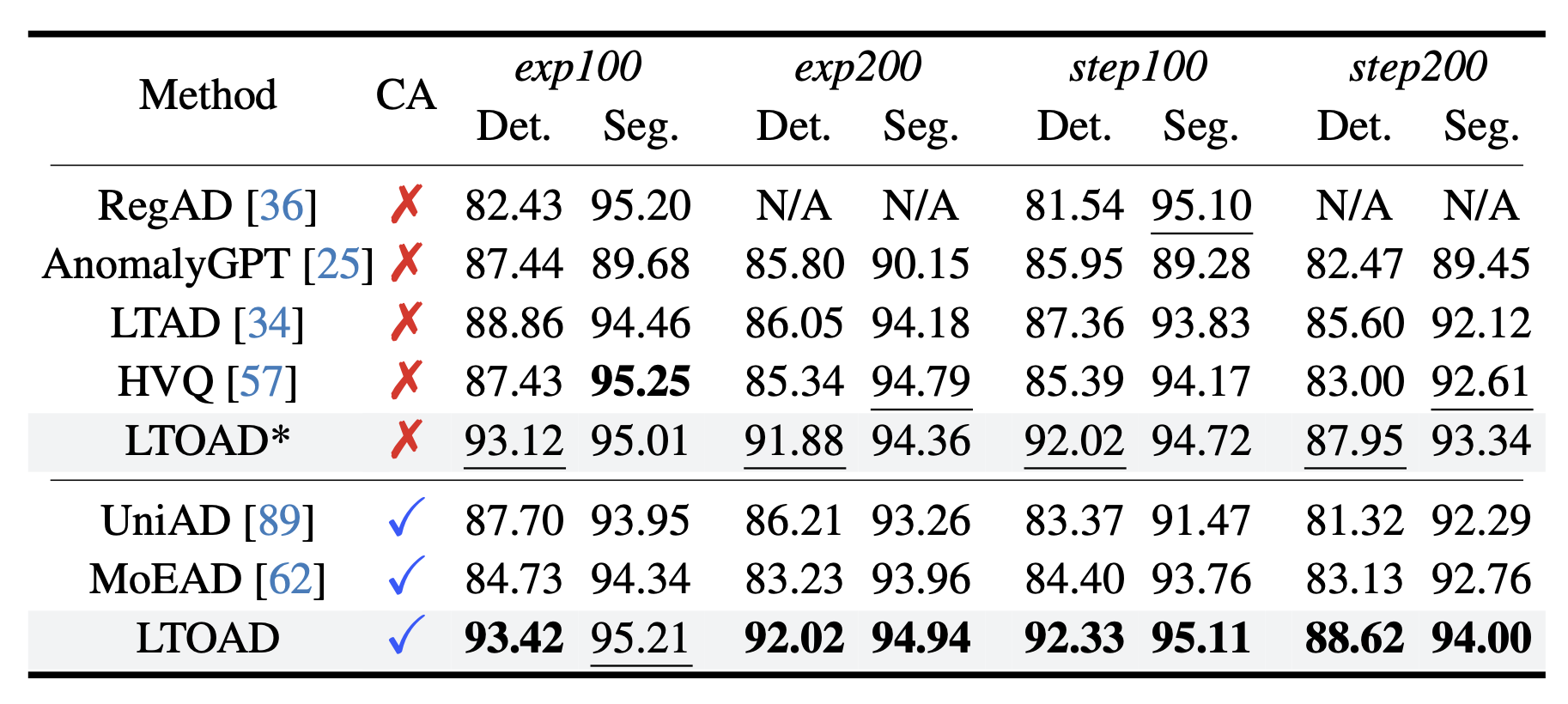
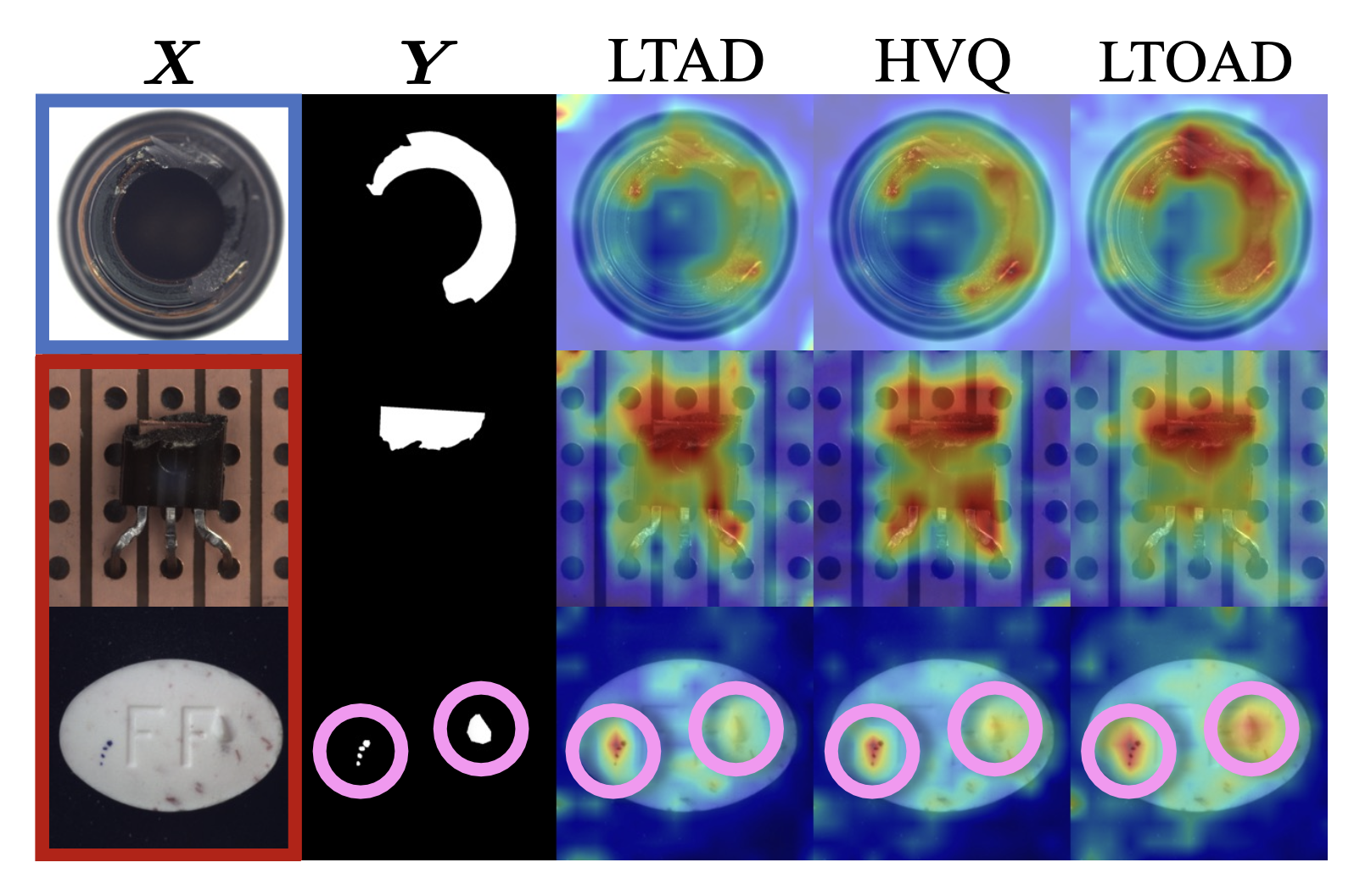
Our class-agnostic LTOAD framework consistently outperform SOTA AD methods on most long-tailed settings. Noted that being class-agnostic is a more challenging setting than not.
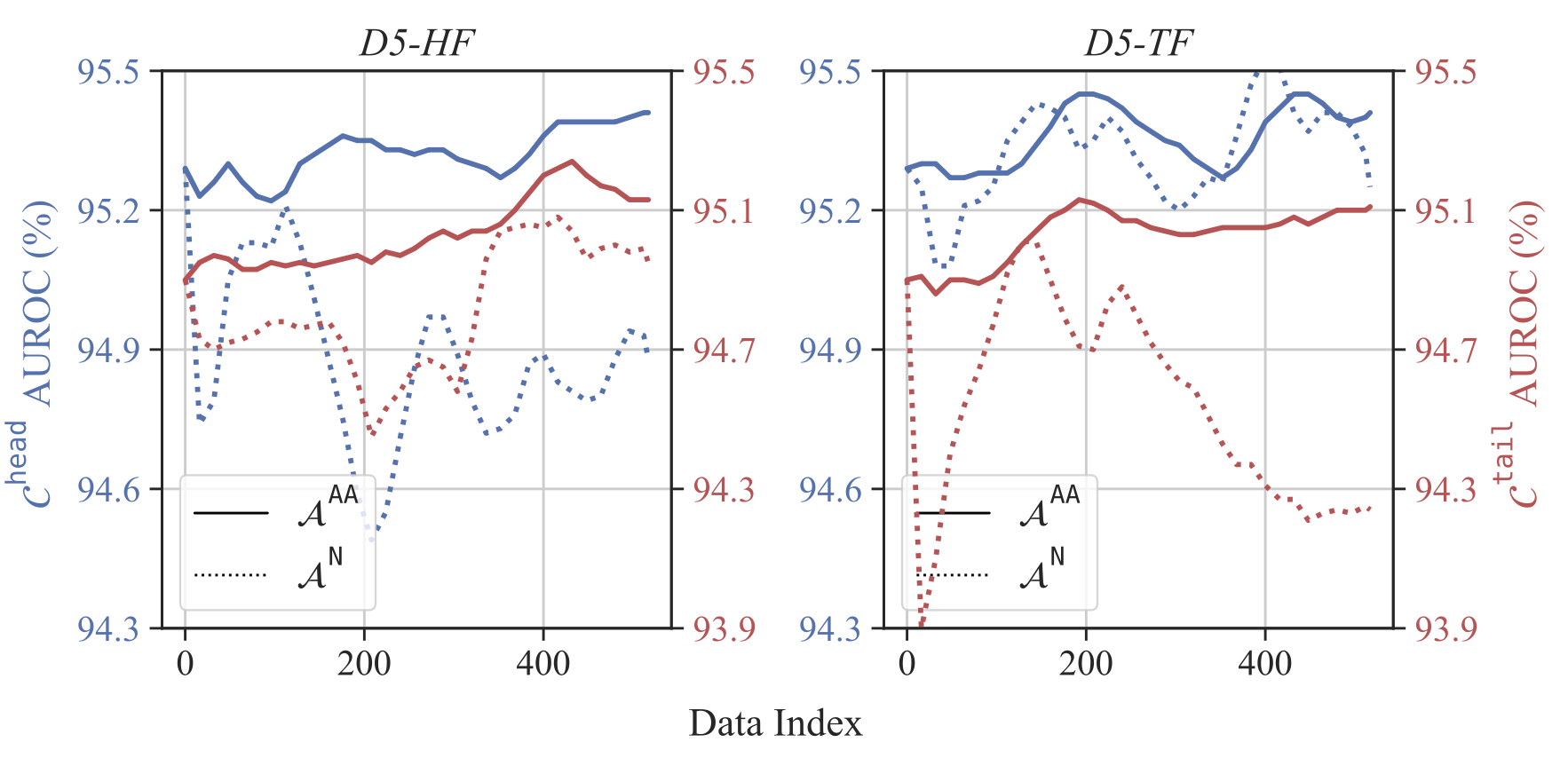
Our online learning algorithm $\mathcal{A}^{\tt AA}$ improves steadily under both D5-HF and D5-TF
while the baseline $\mathcal{A}^{\tt N}$ falls off during later steps.
Citation
@inproceedings{yang2025ltoad,
title={Toward Long-Tailed Online Anomaly Detection through Class-Agnostic Concepts},
author={Yang, Chiao-An and Peng, Kuan-Chuan and Yeh, Raymond A.},
booktitle={Proc. ICCV},
year={2025}
}